planck remplaça les constantes empiriques c et c par des constantes naturelles : la constante de boltzmann, la vitesse de la lumière dans le vide et une nouvelle constante h nommée constante de planck. il développa ensuite en quelques sees la loi du rayonnement de planck, qui marque le début de la mécanique en physique, la loi du déplacement de wien, ainsi nommée d'après son découvreur wilhelm wien, est une loi selon laquelle la longueur d'onde à laquelle un corps noir émet le plus de flux lumineux énergétique est inversement proportionnelle à sa température. la loi de wien se déduit de la loi de planck du rayonnement une fois simplifiée, avec la constante de boltzmann kb égale à , x j.k, c la vitesse de la lumière dans le vide (approximativement , x m.s) et h la constante de planck (, x m.kg/s), on obtient la loi de wien précédemment évoquée. la loi peut alors s'écrire

Vu sur upload.wikimedia.org
.jpg)
Vu sur slideplayer.fr

Vu sur s1.studylibfr.com
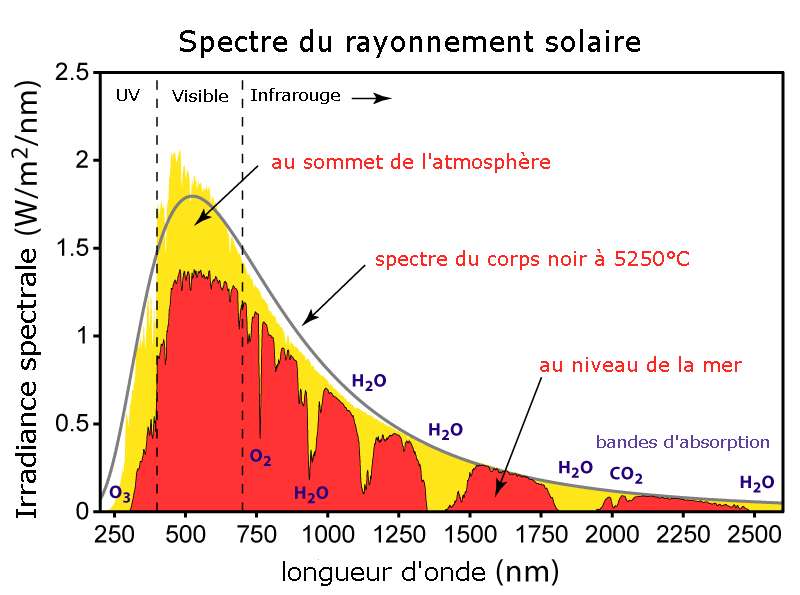
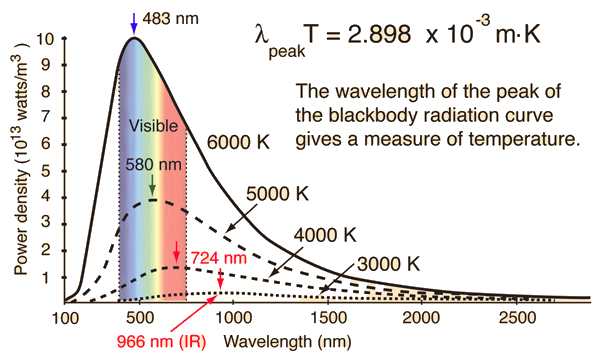
slt en physique on a abordé l'astrophysique on a vu que pour détérminer la t&#; d'un astre ou d'une étoile il suffit d'utiliser la loi de wien qui est lambda=a/t avec t en kelvin tenant j'aimerai savoir quelle est a =la constante de wien= ,.(exp) nm k(exp) je veux dire en quoi consiste elle ds wilhelm wien a remarqué que la longueur d'onde correspondante au maximum de rayonnement était inversement proportionnelle à la température du corps noir. d'où la célèbre loi de wien : t w σ λ = max. où σw est une constante égale à ,. m.k. . en appliquant la loi de wien aux objets suivants, calculer la où c correspond à la vitesse de la lumière dans le vide, h est la constante de planck, k la constante de boltzmann, \lambda la longueur d'onde à laquelle le rayonnement est émis et t la température de surface du corps noir. la figure ci dessous montre le comportement de e(\lambda) pour différente température de surface
Vu sur 230nsc1.phy-astr.gsu.edu

Vu sur image.slidesharecdn.com

Vu sur upload.wikimedia.org
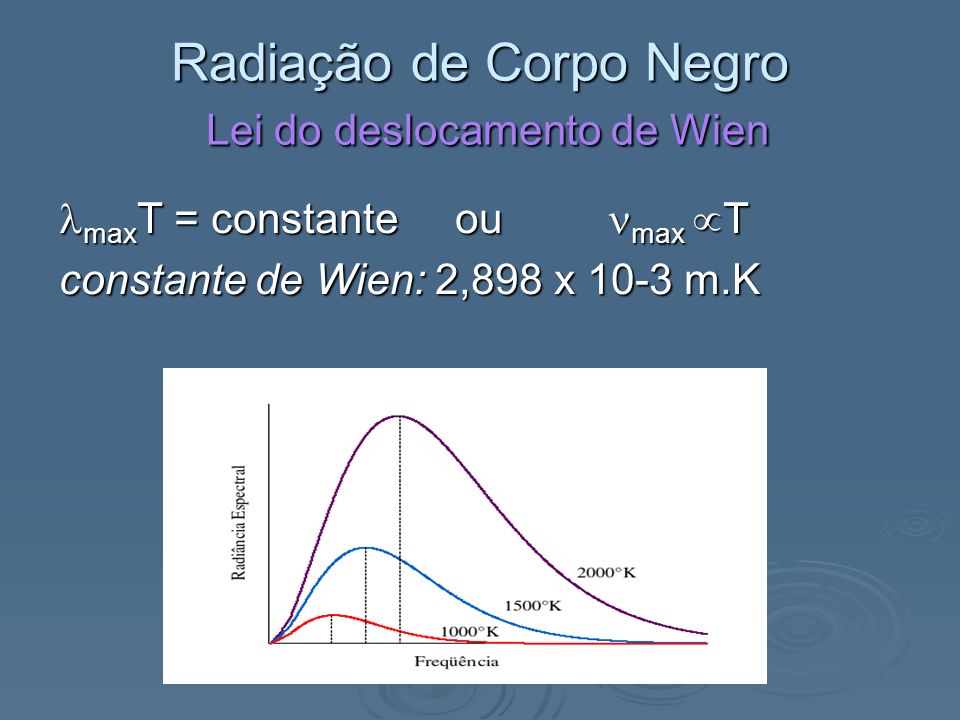
la loi de déplacement de wien. le calcul du maximum d'intensité de la courbe de luminance spectrale du corps noir passe par une dérivation de cette _{\mathrm{max}} la longueur d'onde du maximum de luminance spectrale, il apparaît donc : \lambda _{\mathrm{max}}\ t\ = \ \. le calcul de cette constante donne :. la réponse vient de l'analyse de la répartition de l'intensité lumineuse du spectre de chacune de ces étoiles. de cette analyse, on tire la valeur de la longueur d'onde pour laquelle on note le maximum en intensité lumineuse : λmax puis on applique la loi de wien : t = ,. λmax avec : t : température elle est reliée à la température du corps rayonnant par une relation, nommée loi du déplacement de wien, ou plus simplement loi de wien : la longueur d'onde est exprimée en mètre. la température t est en kelvin. la constante est quant à elle en (mètre kelvin). une température en degré kelvin est obtenue en ajoutant #eanf#

Vu sur slideplayer.fr

Vu sur fracademic.com
Vu sur slideplayer.com.br

Vu sur docplayer.fr