en physique, une transformation de galilée correspond aux formules de transformations des coordonnées spatiales et temporelle entre deux référentiels galiléens donnés. tout référentiel en mouvement de translation rectiligne et uniforme par rapport à un référentiel donné supposé galiléen, est luimême galiléen.
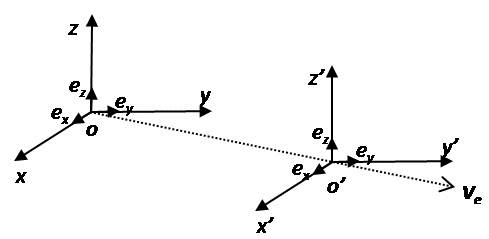
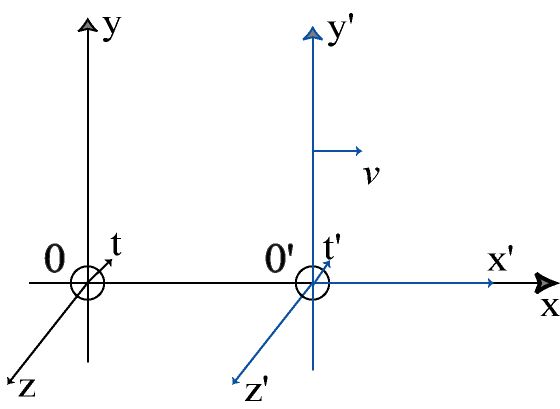
mai transformation de galilée. • référentiel d’inertie r: repère oxyz avec une horloge placée on o mesurant le temps t. • référentiel d’inertie r’ en. « saut de vitesse standard v » par rapport à un référentiel d’inertie r. repère o’x’y’z’ avec une horloge placée on o’ mesurant le temps t’. à t=, les deux
chapitre temps et relativité ) transformation de galilée ce chapitre explique les limités de la transformation

Vu sur upload.wikimedia.org
Vu sur res-nlp.univ-lemans.fr
Vu sur slideplayer.fr
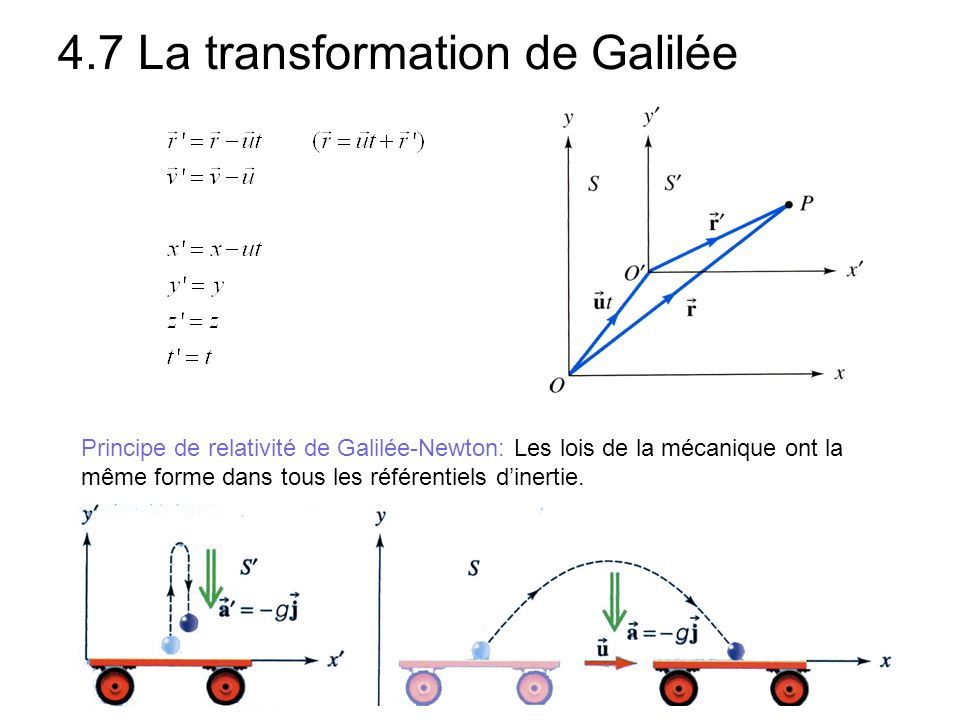
transformation de galilée et temps absolu. pour les phénomènes de mécanique classique, le problème posé cidessus de l’ l’invariance de forme des relations entre grandeurs physiques avait été formulé par les fondateurs de la mécanique classique, en particulier newton. fondamental : la première loi de newton
les transformations de galilée et de lorentz établissent des relations entre les coordonnées associées `a deux référentiels en translation l’un par rapport `a l’autre. la transformation de galilée était une conséquence des lois de la mécanique classique. `a la fin du xixe si`ecle, le développement de la théorie de l’
que devient un loi physique lorsqu’on l’exprime dans deux repères différents: l’un supposé au repos et l’autre en mouvement. le repère au repos estil plus légitime que celui en mouvement? voyons cela d’un peu plus près. pour un certain repère (x, y, z) au repos tu écris que la composante de la force

Vu sur i.ytimg.com
Vu sur culturesciencesphysique.ens-lyon.fr
Vu sur logiqueformelle.free.fr
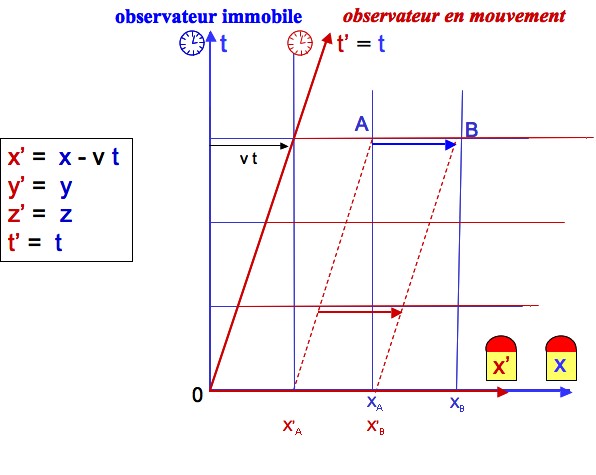
la transformation de galilée préserve la simultanéité. de la même manière, la transformation préserve les mesures de longueur : si à un instant donné on mesure la longueur d’un objet dans r, on trouvera une réponse identique si on réalise la mesure dans r’. ces deux propriétés sont bien pratiques
, quelqu’un sauraitil me démontrer que les lois de newton sont invariantes par transformations de galilée ? ps : si cette même personne (
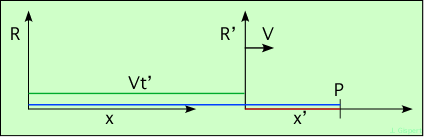
puisque le cadre choisi concerne les référentiels galiléens, il faut déterminer comment passer d’un référentiel galiléen à un autre (par conséquent se déplaçant à vitesse constante par rapport au premier). la transformation de galilée permet de calculer les coordonnées dans un référentiel o, d’un point
#eanf#

Vu sur slideplayer.fr
Vu sur astronomia.fr
Vu sur physique-chimie.gjn.cz

Vu sur semsci.u-strasbg.fr










