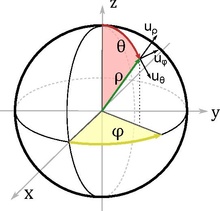
on appelle coordonnées sphériques divers systèmes de coordonnées de l’espace qui généralisent les coordonnées polaires du plan. un point de l’espace y est repéré par la distance à un pôle et deux angles. ce système est d’emploi courant pour le repérage géographique : l’altitude, la latitude, et la longitude sont une 
les coordonnées sphériques (voir figure ) permettent de repérer un point sur une sphère de rayon . c’est typiquement le repérage d’un point sur la terre pour lequel il suffit alors de préciser deux angles : la latitude et la longitude. figure : le système de coordonnées sphériques et la base associée. coordonnées 
en physique mais aussi en géométrie de l’espace, la maitrise des modes de repérage repose sur la

Vu sur upload.wikimedia.org

Vu sur upload.wikimedia.org

Vu sur res-nlp.univ-lemans.fr

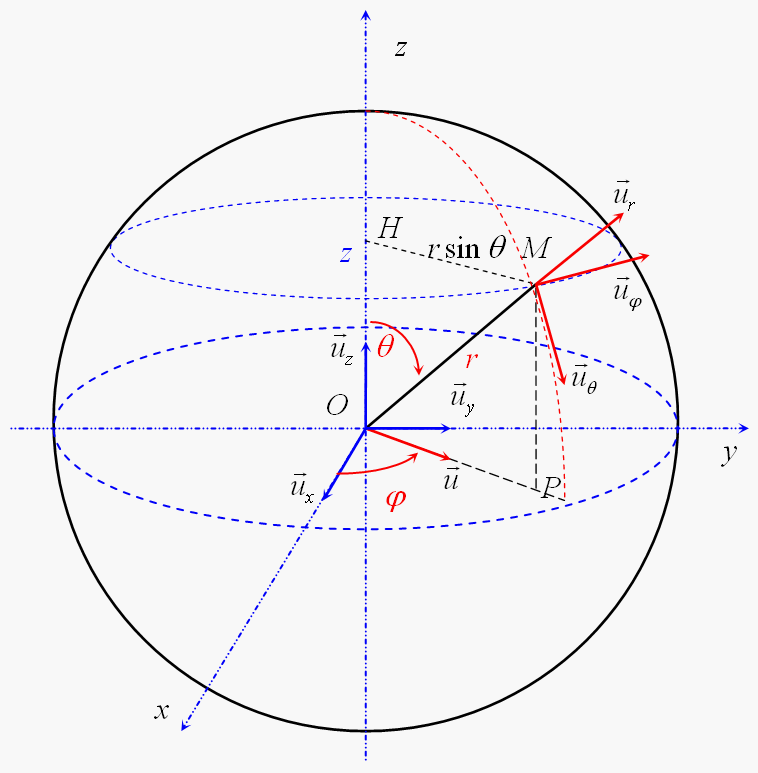
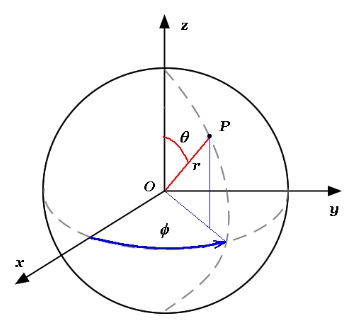
. coordonnées sphériques. .. repérage d’un point en coordonnées sphériques. en coordonnées sphériques, un point m(r) est considéré comme un point d’une sph`ere centrée sur. o. le point m est repéré. • par le rayon r de la sph`ere `a laquelle il appartient. • l’angle θ entre la direction. −→. oz et la direction. −−→.
les coordonnées sphériques. prenons comme exemple un point m repéré à la surface de la terre. la méthode la plus facile pour repérer ce point est l’utilisation de deux angles appelés latitude et longitude. plus généralement, pour tout mouvement de m autour d’un point o particulier, il est préférable.
c’est suffisant si l’on n’a pas besoin d’utiliser simultanément les coordonnées cylindriques et sphériques. pour la même raison, l’angle polaire de \vec e_x avec \overrightarrow {op}, appelé longitude de m, est soit noté \theta (pour conserver la notation du repère cylindrique), soit noté \varphi . enfin, l’angle polaire de \vec 

Vu sur ilemaths.net

Vu sur upload.wikimedia.org

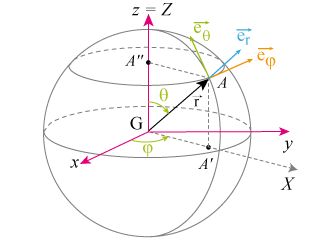
Vu sur res-nlp.univ-lemans.fr

la base et les coordonnées sont définies cidessous : le point est repéré par ses coordonnées sphériques : toujours positif,. dans la base sphérique , le vecteur position s’écrit . coordonnées sphériques. agrandir l’image. coordonnées sphériques. la ligne coordonnée associée à est la droite dont la direction varie avec .
chapitre : systèmes de coordonnées. ) coordonnées sphériques. │. │. ⎩. │. │. ⎨. ⎧. = = = = = = θ. ϕ θ. ϕ θ cos . sin sin . cos sin . rkom z. rjom y. riom x о о о. plus adapté pour repérer un point sur une sphère. les coordonnées de m sont définies par la donnée de r, θ et ϕ. (et non x, y et z). [ ]π θ ,. ∈. [ ]π. ϕ ,. ∈.  
video created by École polytechnique fédérale de lausanne for the course “mécanique de newton”. vous allez apprendre l’art d’exprimer une vitesse et une accélération vectorielles avec des coordonnées généralisées; ça permettra de modéliser plus
#eanf#

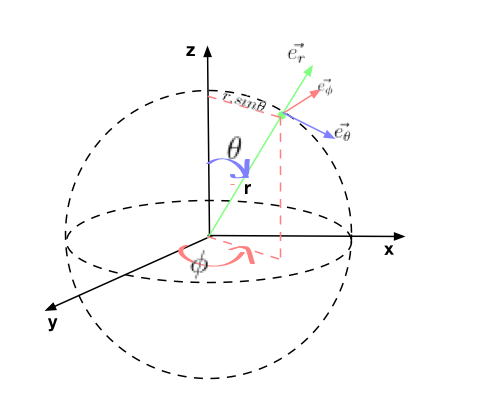
Vu sur monde.de.physique.free.fr

Vu sur epiphys.emn.fr

Vu sur upload.wikimedia.org

Vu sur philippelopes.free.fr