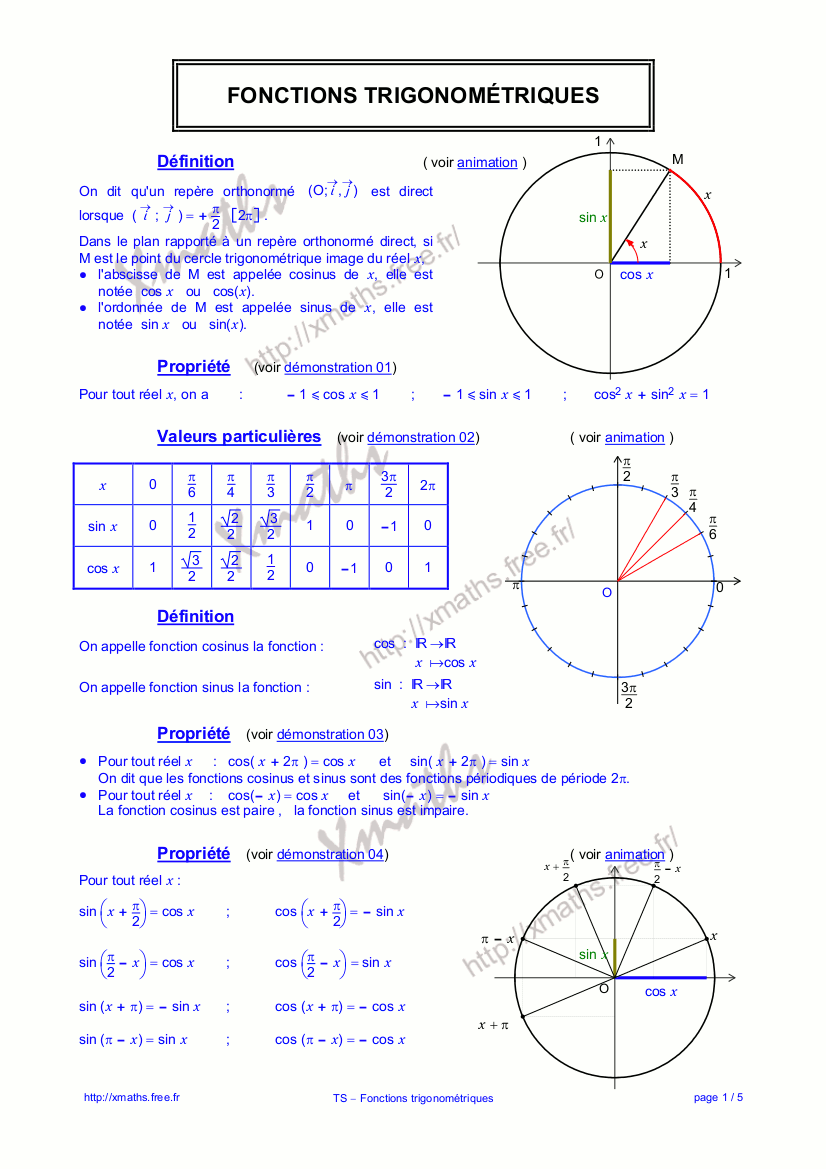
formulaire de trigonométrie circulaire. b cotan(x). k sin(x) мн cos(x) = abscisse de m tan(x) sin(x) = ordonnée de m. Ł tan(x) = ah cos(x) a cotan(x) = bk eix = zm. Π sin(x). pour x É, tz, tan(x) = cos(x). valeurs usuelles. cos(x) et pour x É tz, cotan(x) = . enfin pour x z, cotan(x) = sin(x). z tan(x). x en . x en rd. . sin(x).
la trigonométrie (du grec τρίγωνος trígonos, « triangulaire », et μέτρον métron, « mesure ») est une branche des mathématiques qui traite des relations entre distances et angles dans les triangles et des fonctions trigonométriques telles que sinus, cosinus et tangente.
nombres, curiosités, théorie et usages: toutes les formules de trigonométrie.

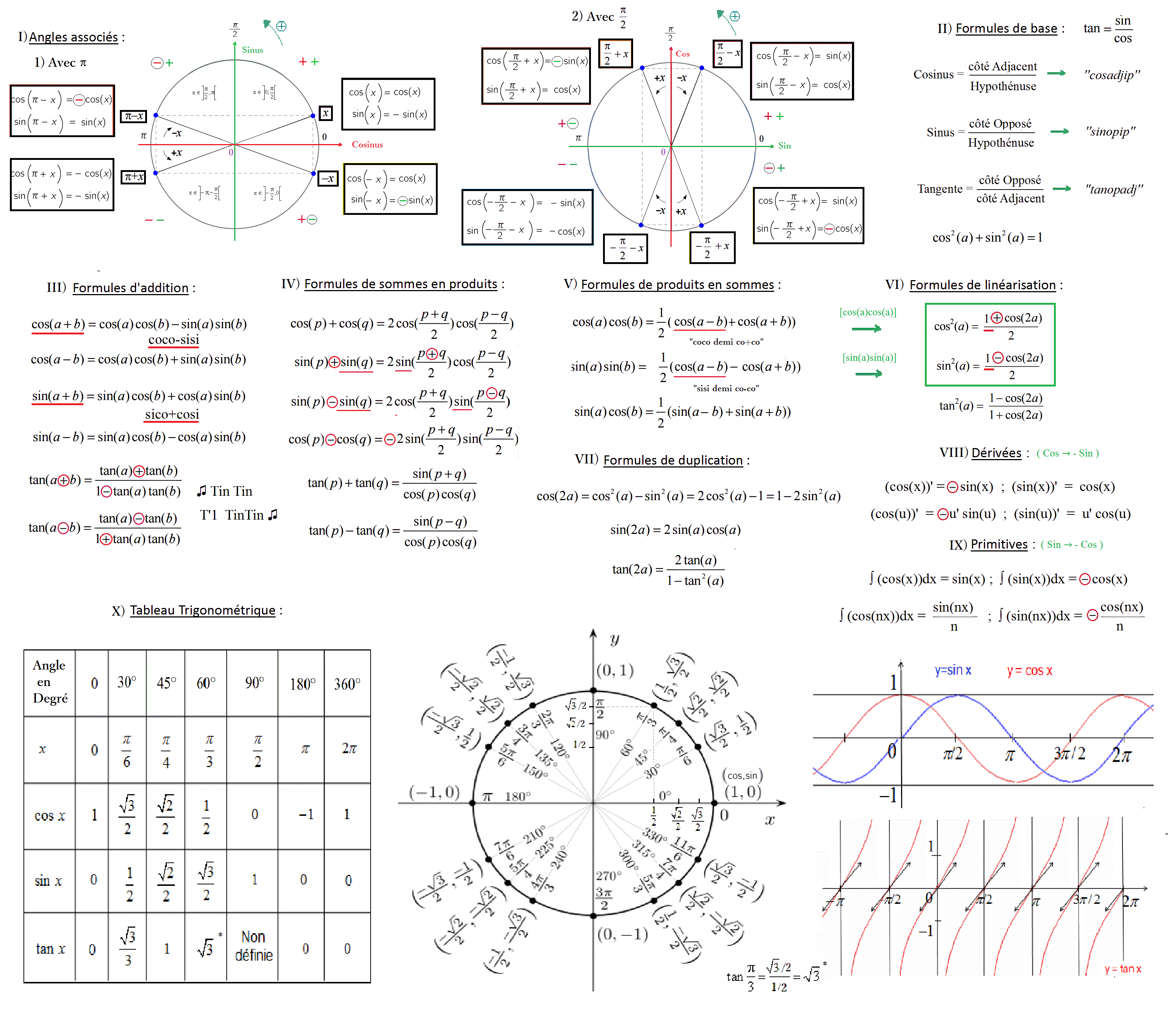
Vu sur jeretiens.net

Vu sur bibmath.net

Vu sur alloprof.qc.ca

. exemple : calcul du sinus à partir du cosinus. propriétés des arcs associés; formules de trigonométrie. . formulaire : addition; . formulaire : duplication; . formulaire : linéarisation (formules de carnot); . formulaire : produitsomme; . formulaire : sommeproduit (formules de 
la trigonométrie, c’est l’une des bases fondamentales qu’il faut maîtriser en maths, elle est partout ! cependant, les formules de trigo ne sont pas si faciles à mémoriser (certes on peut les retrouver grâce à des démonstrations mathématiques, mais cela peut faire perdre du temps, il faut donc les connaître 
mai les moyens mnémotechniques pour mémoriser plus facilement les formules de sinus, cosinus et tangente en trigonométrie ne manquent pas ! le principe est de ne retenir que la première syllabe des motsclés de chaque théorème : cosinus = côté adjacent sur l’hypothénuse » devient cosadjip ou 

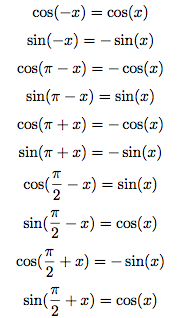
Vu sur mathsbook.fr

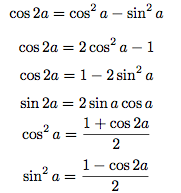
Vu sur mathsbook.fr

Vu sur xmaths.free.fr

formules de trigonométrie circulaire. soient a, b, p, q, x, y ∈ r (tels que les fonctions soient bien définies) et n ∈ n. la parfaite connaissance des graphes des fonctions trigonométriques est nécessaire. relations fondamentales cos(x) sin(x)=. − d dx cotan(x) = cotan(x) = sin(x) d dx tan(x) = tan(x) = .
on rappelle ici et on complète les résultats énoncés au lycée. l’objectif à viser est la technicité. pour cela, il faut : Œ connaître par cœur les différentes formules de trigonométrie, savoir à quel moment s’en servir. en ce qui concerne le premier point (Œ), au cours de l’année de mathématiques supérieures, on doit apprendre 
cos(x) = sin(x) = = sin²(q) cos²(q). sin(q) = sin(q) sin(q p) = sin(q) sin(p q) = sin(q). cos(q) = cos(q) cos(q p) = cos(q) cos(p q) = cos(q). tan(q) = tan(q) tan(q p) = tan(q) tan(p q) = tan(q). sin( ) = cos(q) sin( ) = cos(q). cos( ) = sin(q) cos( ) = sin(q). formules de transformations produitssommes. addition.
cours de trigonométrie de troisième pour apprendre à nommer les côtés d’un triangle rectangle, apprendre les trois formules et apprendre à les utiliser.

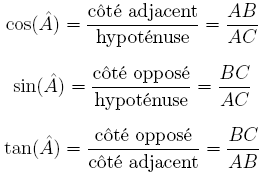
Vu sur trigofacile.com

Vu sur dundee.pagesperso-orange.fr

Vu sur journals.openedition.org

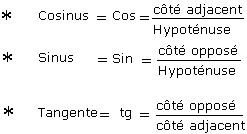
Vu sur positron-libre.com