l'orbite géostationnaire d'un satellite artificiel est parcourue par le satellite avec une période égale à celle de rotation de la terre, c'estàdire d'un jour. il est facile de retrouver la valeur de son rayon, si l'on se. souvient de la troisième loi de kepler, appliquée à l'ensemble des satellites de la terre: at = gmtml/ = cte.

Vu sur e.m.c.2.free.fr
Vu sur chimix.com
nota: pour la ° orbite (no = ) le rayon lr vaut ,. m. une orbite stationnaire concerne celle sur laquelle s'établit un électron (son moment cinétique est n fois h/ et il ne rayonne pas). orbitale atomique. une orbitale atomique est la probabilité de présence d'un électron lié, autour du noyau d'un atome donné. aller à relations entre les anomalies et les rayons si on utilise une valeur initiale e = π {\displaystyle e_{}=\pi } e_{}=\pi , la convergence est garantie, et est toujours très rapide (dix chiffres significatifs en quatre itérations). les catégories d'orbite des satellites artificiels selon l'altitude (schéma à l'échelle).
Vu sur upload.wikimedia.org
l'orbite géostationnaire, abrégée geo (geostationary orbit) est une orbite circulaire autour d'un corps céleste (terre ou autre) caractérisée par une inclinaison orbitale nulle et une vitesse orbitale identique à celle de ce corps. un objet placé sur une orbite géostationnaire reste en permanence audessus du même point de quand un satellite se déplace sur une orbite géosynchrone autour de la terre, il a besoin de se déplacer à un certain rayon orbital et la période pour tenir cette orbite. parce que le rayon.

Vu sur eduscol.education.fr
Vu sur media4.obspm.fr
masse ( kg). ,. rayon moyen (km). ,. rayon équatorial (km). ,. rayon polaire (km). ,. rayon du noyau (km). . aplatissement. ,. volume ( km) ,. excentricité de l'orbite. ,. inclinaison sur l'écliptique (°). ,. longitude du noeud ascendant (°). ,. sans émission de rayonnement, les électrons ne peuvent graviter autour du noyau que sur certaines orbites permises. cellesci sont déterminées par la condition de quantification suivante : π. = h n rmvnn avec : n = nombre quantique principal, n ∈ { ; ; ; } m = masse de l'électron rn = rayon de l'orbite de l'électron

Vu sur upload.wikimedia.org
la relation donnant la vitesse orbitale en fonction du rayon d'une orbite circulaire permet, comme la e loi de kepler, de "peser" la masse m du centre de force. rien d'étonnant à cela, il s'agit de la même loi réécrite sous une autre forme (voir exercice). la mesure des observables v et r permet de déterminer la masse m calcul du diamètre de la lune et du rayon de son orbite. philippe drompt, gymnase français de bienne. résumé. cet article vous propose une méthode expérimentale, à partir d'une photographie, pour déterminer le diamètre de la lune et la distance terrelune. c'est une manière simple, en utilisant des moyens
Vu sur astropolis.fr
#eanf#

Vu sur slideplayer.fr

Vu sur web-sciences.com
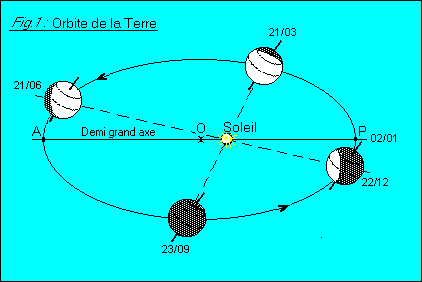
Vu sur pfz.free.fr