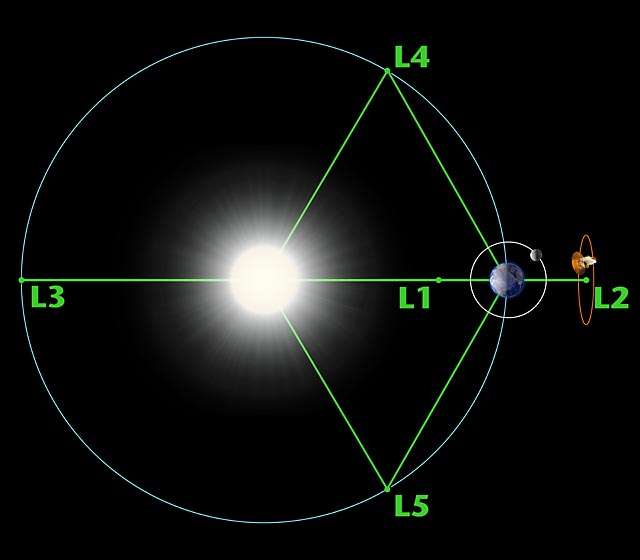
un point de lagrange (noté l à l), ou, plus rarement, point de libration, est une position de l'espace où les champs de gravité de deux corps en mouvement orbital l'un autour de l'autre, et de masses substantielles, fournissent exactement la force centripète requise pour que ce point de l'espace accompagne un point de lagrange est une position de l'espace dans un système à deux corps, où leurs champs de gravité se combinent de manière à fournir un point d'équilibre à un troisième corps de masse les points de lagrange sont des positions de l'espace où les champs de gravité de deux corps en orbite l'un autour de l'autre fournissent exactement la force centripète requise pour que ce point de l'espace accompagne simultanément la rotation des deux corps. ils sont nommés en l'honneur du mathématicien français
Vu sur fr.cdn.v5.futura-sciences.com
Vu sur static.le-systeme-solaire.net

Vu sur hatteras.free.fr
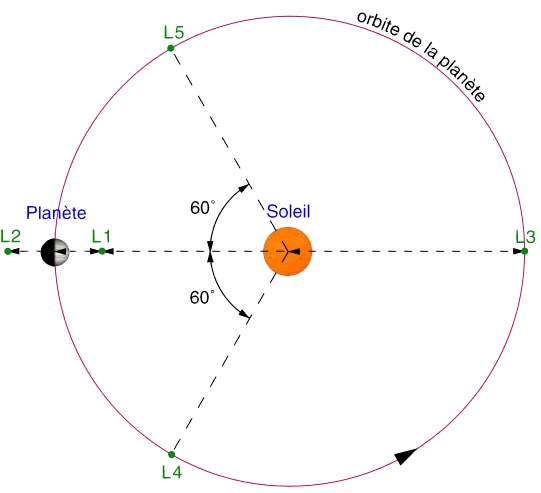
l'un des aspects de la mécanique céleste qui a occupé mathématiciens et physiciens pendant plusieurs siècles est la recherche de solutions au problème des trois corps, l'analyse du mouvement relatif de trois corps sous l'influence de la force gravitationnelle. le cas particulier le plus pertinent est celui un "point de lagrange" (noté l), ou "point de libration", est une position de l'espace où les champs de gravité de deux corps en orbite l'un autour de l'autre, et de masses substantielles, se combinent de manière à fournir un point d'équilibre à un troisième corps de masse négligeable, tel que les positions relatives des trois nombres, curiosités, théorie et usages: astronomie: les points de lagrange.

Vu sur planete.gaia.free.fr
Vu sur upload.wikimedia.org

Vu sur upload.wikimedia.org
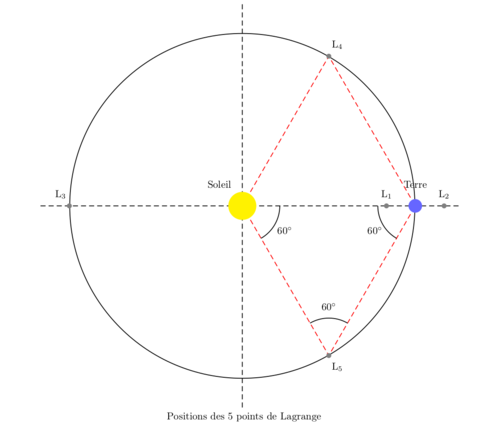
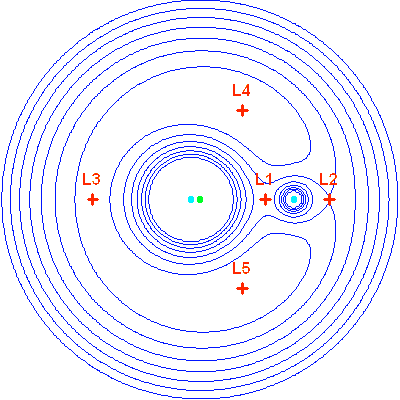
le point de lagrange est un point privilégié de l'espace, décrit en par josephlouis de lagrange ( − ). le mathématicien italofrançais a découvert l'existence de positions d'équilibre, où les champs de gravité entre objets massifs par exemple le soleil et la terre, se compensent. un point les points de lagrange par gilbert gastebois. a. les points de lagrange. mo : soleil ( mo represente la masse et la position du soleil ). m : terre ( m represente la masse et la position de la terre ). o : barycentre des masses mo et m m : masse de l'astéroïde a = mom. m<<mo et m<<<m ( on néglige l'influence de m sur m dans le plan orbital, les équipotentielles du champ montrent point d'équilibre. trois de ces points (l, l et l) sont des selles. l et l sont des maxima. nasamap.jpg. position des points de lagrange du système soleilterre, et orientation du champ gravitationnel en leur voisinage. crédit : nasa/wmap points de lagrange. dans le cadre du problème à trois corps réduit (c'estàdire dans lequel l'un des corps est considéré de masse négligeable), on est conduit à considérer des points situés sur le plan orbital défini par deux corps célestes en mouvement autour d'un centre de masse commun, et pour lesquels la somme

Vu sur astronomie.coursgratuits.net

Vu sur planetastronomy.com

Vu sur sciencetonnante.files.wordpress.com
Vu sur media4.obspm.fr