formule trigonométrique : cosinus. en ème, on a découvert un nouvel outil appelé « cosinus ». cet outil s’utilise uniquement dans les triangles rectangles. le cosinus d’un angle aigu est égal au rapport : ce rapport ne dépend que de la mesure de l’angle considéré. la valeur du cosinus d’un angle est toujours comprise

Vu sur i.ytimg.com

Vu sur educastream.com
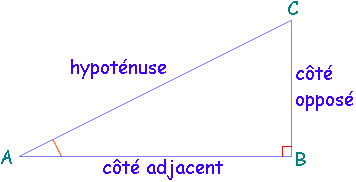
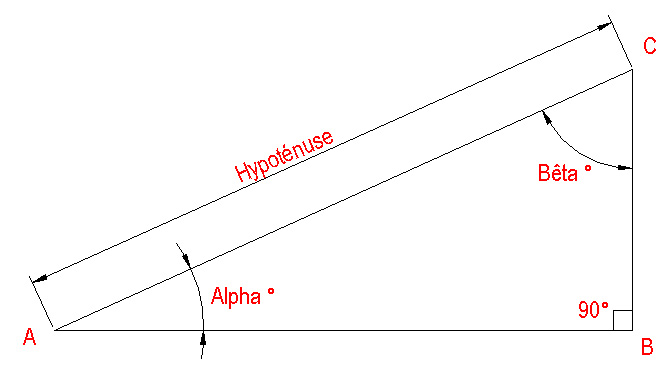
À suivre : relations trigonométriques et longueur des côtés d’un triangle rectangle opposeˊ a a a b b b c c c. il faut bien comprendre que les mots hypoténuse, opposé et adjacent désignent les longueurs de l’hypoténuse, du côté opposé ou du côté adjacent à l’angle concerné. acronyme, description, formule
figure & notations. >>> angles et côtés. >>> aire du triangle. >>> cercles. >>> droites. >>> loi des sinus. >>> loi des cosinus. >>> loi des projections. >>> loi des demiangles. >>> loi de napier. >>> loi des tangentes. >>> loi des cotangentes. >>> formule de mollweide. >>> médianes. >>> exemple de résolution
Vu sur editions-petiteelisabeth.fr
si on connaît deux côtés d’un triangle rectangle, on peut calculer la mesure des trois angles. soit abc un triangle rectangle en a.on donne : [ab] = et [ac] = .on veut calculer la mesure des angles et.ici, on connaît [ac], le côté opposé à l’angle et [ab], le côté adjacent à l’angle.on va donc utiliser pour calculer. • calcul
. cosinus, sinus, tangente. le cosinus, le sinus et la tangente sont des outils qui permettent de calculer les longueurs et la mesure des angles d’un triangle. les formules en ce qui concernent le triangle rectangle cidessous sont les suivantes :
Vu sur trigofacile.com

Vu sur s4.e-monsite.com
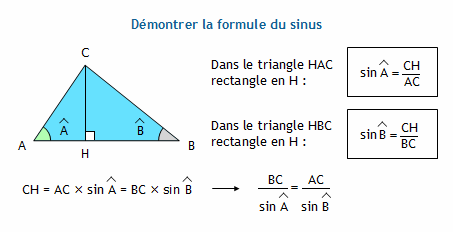
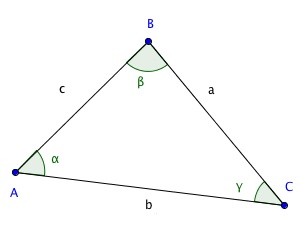
calculons les longueurs des cotés et la mesure des angles dans un triangle quelconque grâce aux relations trigonométriques en ligne. autres formules : lois des sinus. le calculateur utilise aussi les formules, appelées « loi des sinus », valables dans un triangle quelconque : a sin(α) = b sin(β) = c sin(γ)
théorème d’alkashi, somme des angles d’un triangle, loi des sinus, formule de héron, formule des aires.

Vu sur debart.pagesperso-orange.fr
aller à deux angles et le côté commun dans un triangle où deux angles α et β sont connus, ainsi que le côté commun à ces angles c, le dernier angle s’obtient par la formule d’alkashi et les deux derniers côtés par les analogies de napier. les formules pour l’angle manquant et les côtés ressemblent à celles du
aller à exemple : calcul d’un angle à partir du côté adjacent et de l pour avoir une précision au degré près pour l’angle, il est conseillé de garder au moins trois décimales pour le cosinus. la notation c o s − {\displaystyle cos^{}} cos^{} est mauvaise mais nous la gardons car elle apparaît sur les
Vu sur i70.servimg.com
si on connaît la mesure d’un angle et la mesure des deux côtés formant l’angle, on utilise la formule trigonométrique. formule : a = côté de l’angle x côté de l’angle x sinus de l’angle. . démonstration : la formule de l’aire d’un triangle est a = bxh. la base vaut b. pour trouver h, utilisons la fonction sinus : sin z = a h.
Vu sur calculis.net
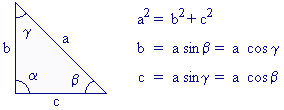
Vu sur astrosurf.com
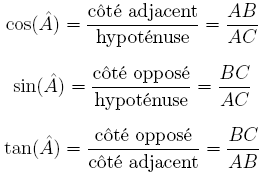
Vu sur trigofacile.com









