l’excentricité orbitale définit, en mécanique céleste et en mécanique spatiale, la forme des orbites des objets célestes. . [masquer]. notation et types d’orbites; notions connexes. . vecteur excentricité; . angle d’excentricité; . aplatissement. historique; calcul de l’excentricité d’une orbite
Vu sur acces.ens-lyon.fr

Vu sur upload.wikimedia.org
en géométrie, une ellipse est une courbe plane fermée obtenue par l’intersection d’un cône de révolution avec un plan, à condition que celuici coupe l’axe de rotation du cône ou du cylindre : c’est une conique d’excentricité strictement comprise entre et . on peut également la définir comme le lieu des points dont la
en mathématiques, l’excentricité est un paramètre réel positif caractéristique d’une courbe conique. elle est en général notée e. en fonction des valeurs de e on obtient pour : e = , un cercle; < e < , une ellipse; e = , une parabole; e > , une hyperbole. sauf pour le cercle, l’excentricité est le nombre positif e

Vu sur upload.wikimedia.org
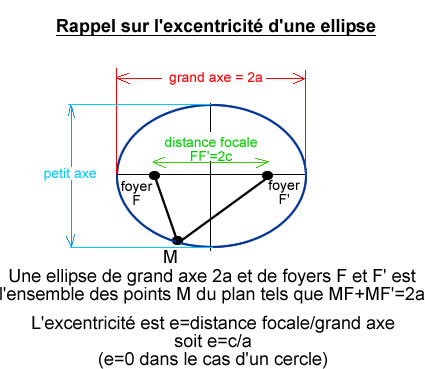
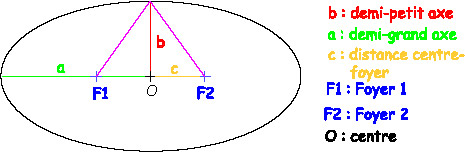
paramètres : ac : grand axe. bd : petit axe. o : centre. f et f’ : foyers a : longueur du demi grand axe b : longueur du demi petit axe c : distance du centre au foyer e : excentricité e = c/a. pour tout point m de l’ellipse mfmf’=a. pour une ellipse l’excentricité est comprise entre et .
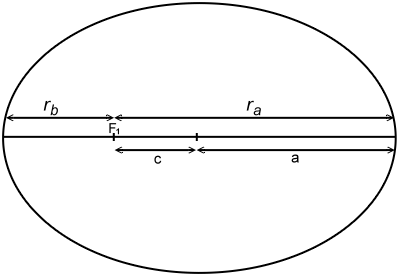
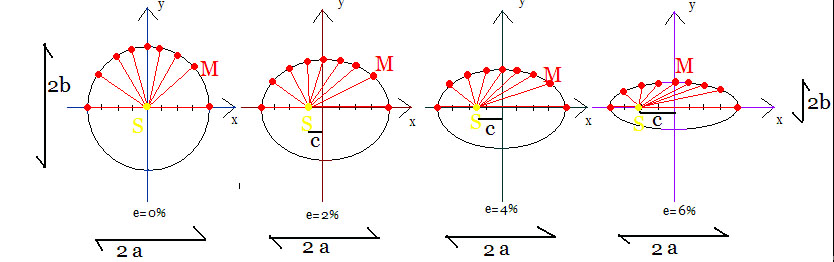
l’excentricité « e » définit la forme des orbites des objets célestes. excentricité. pour les orbites elliptiques, l’excentricité d’une orbite pour être calculée en fonction de son aphélie et de son périhélie : e=/[(r_a/r_p)]. où : ra est le rayon à l’apoapse; rb est le rayon au périapse. l’excentricité d’une orbite peut aussi se

Vu sur eduscol.education.fr
Vu sur planet-terre.ens-lyon.fr
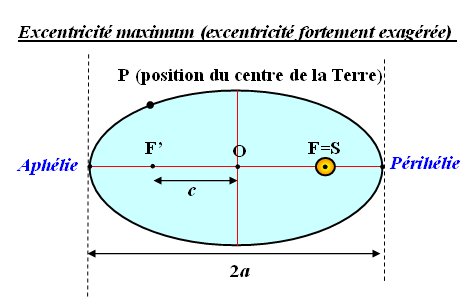
dans le référentiel héliocentrique, la terre décrit une trajectoire elliptique dont le soleil est l’un des foyers (points f et f’ sur le schéma). le grand axe (a) de cette ellipse ne varie pas, il garde sensiblement la valeur km. l’excentricité notée e caractérise l’aplanissement de l’ellipse par rapport à un cercle.
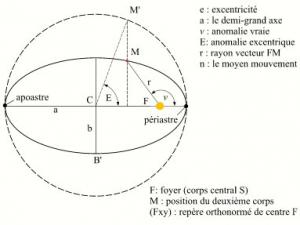
Équation cartésienne réduite : . a = demi grand axe ³ b = demi petit axe > . = demidistance focale. = excentricité, p = = paramètre, coefficient d’aplatissement (par rapport au cercle de rayon a). f(c, ) et f'(c, ) : foyers de l’ellipse. (d), (d’), droites d’équation : directrices de l’ellipse. k : pied de la directrice sur l’axe ox.
Vu sur media4.obspm.fr
r = dist(f,p) = e dist(p,l) dist(p,l) = d r cos θ. donc r = e [d r cos θ ] r [ e cos θ] = ed r = e d /[ e cos θ ] l’équation d’une ellipse en coordonnées polaires est donc: r = p/( e cosθ) = a( e)/( e cosθ) avec p = ed = a( e) e est l’excentricité de l’ellipse et d est la distance entre la directrice est le foyer de l’ellipse.
une excentricité proche correspond à un applatissement maximal. entre ces deux valeurs, l’orbite est elliptique. a exactement, c’est une parabole. au delà de , elle est une hyperbole. cercle, ellipse, parabole et hyperbole sont appelée de coniques. si l’on note e l’excentricité, a et b les deux demiaxes d’une orbite
Vu sur static.le-systeme-solaire.net
la terre décrit dans l’espace, non pas un cercle mais une ellipse, dont le soleil occupe l’un des foyers, mais cette ellipse se déforme, jusqu’à une excentricité maximum de ,. elle est actuellement de , et la distance terre soleil varie de , environ millions de km. dans le système solaire, les

Vu sur eduscol.education.fr
Vu sur coreana.fr
Vu sur simlex.free.fr









