l’immeuble est composé de niveaux et d’un toit. on peut exprimer la hauteur du toit en fonction de celle d’un étage. on choisira donc comme inconnue la hauteur d’un étage. on notera h cette inconnue. soit h la hauteur d’un étage ( en mètres ). ② ème étape : mise en Équation du problÈme. si la hauteur d’un
) elsa achète assiettes plates, assiettes creuses et assiettes à dessert. une assiette creuse coûte de moins qu’une assiette plate. une assiette à dessert coûte de moins qu’une assiette plate. elle dépense en tout . quel est le prix de chaque sorte d’assiette ? appeler x le prix d’une assiette plate. alors
exercice . le réservoir d’une voiture est vide aux deux yiers . on ajoute litres de carburant pour le remplir aux trois quarts. mettre en équation ce probléme pour calculer la contenance du réservoir. exercice . un particulier partage son capital en trois parts et effectue les placements suivants :

Vu sur reviseo.com

Vu sur i.ytimg.com

Vu sur reviseo.com
a. un père dispose de pour ses trois enfants. il veut que l’aîné ait de plus que le second et que le second ait de plus que le dernier. quelle somme doit il donner à chacun ? choix de l’inconnue: soit x la somme donnée au dernier (par exemple) mise en équation : le dernier a x le deuxième a x
mettre un problème en équation (). trois cousins, zoé, luc et serge ont à eux trois ans. quel est l’âge de chacun, sachant que luc a le triple de l’âge de zoé et que serge a dix ans de moins que luc ?
dans cette vidéo, tu vas apprendre à mettre un problème en équation pour résoudre ce problème. site officiel

Vu sur reviseo.com

Vu sur i.ytimg.com

Vu sur slideplayer.fr
équation du second degré trouver un rectangle connaissant périmètre et aire première sessti duration:
ici, il s’agira de traiter la résolution de problèmes à l’aide d’équations, conformément au programme officiel de la classe de ème . l’accent est alors mis sur l’enchaînement des étapes de résolution de tels problèmes, c’estàdire : mise en équation, résolution de l’équation et interprétation du résultat. ce cours demande à
un père a ans, son fils a ans. on cherche dans combien d’années le père aura juste fois l’âge de son fils. on désigne par x le nombre d’années pour que le père ait juste trois fois l’âge de son fils. quelle équation permet de traduire l’énoncé ? cochez la bonne réponse.
aller à exemple : mise en équation d’un problème géométrique deuxième étape : on met en équation en exprimant les données du problème en fonction de x. l’aire du carré abcd est x et l’aire du triangle abe est (x.) le problème devient alors de trouver x tel que ces deux aires soient égales,

Vu sur reviseo.com

Vu sur mathovore.fr

Vu sur i.skyrock.net
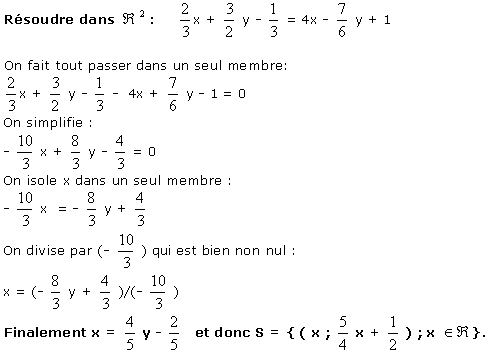
Vu sur keepschool.com









