Vu sur xmaths.free.fr
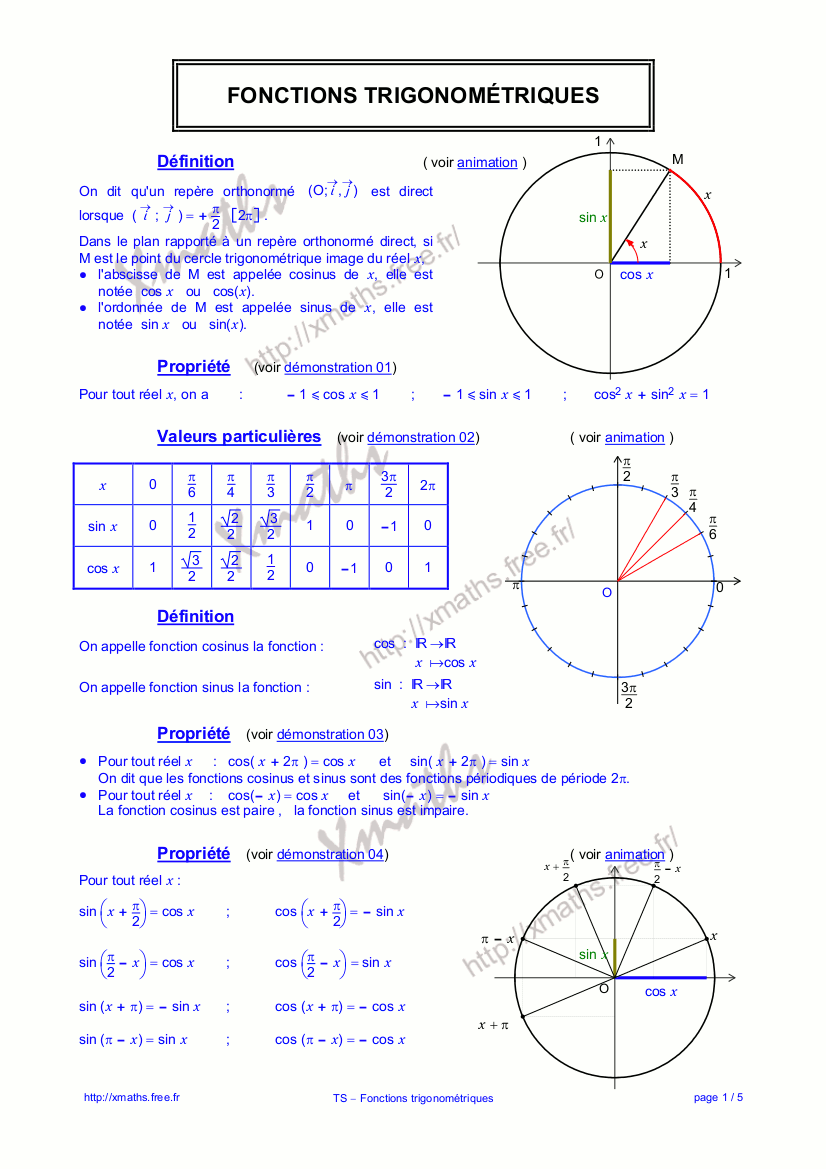
iie c,d math i trigonométrie. . chapitre i. trigonometrie. ) le cercle trigonométrique. • un cercle trigonométrique est un cercle c de rayon qui est orienté, ce qui veut dire qu’on a choisi un sens positif (celui des rondspoints) et un sens négatif (celui des aiguilles d’une montre) : • soit c un cercle
Vu sur xmaths.free.fr
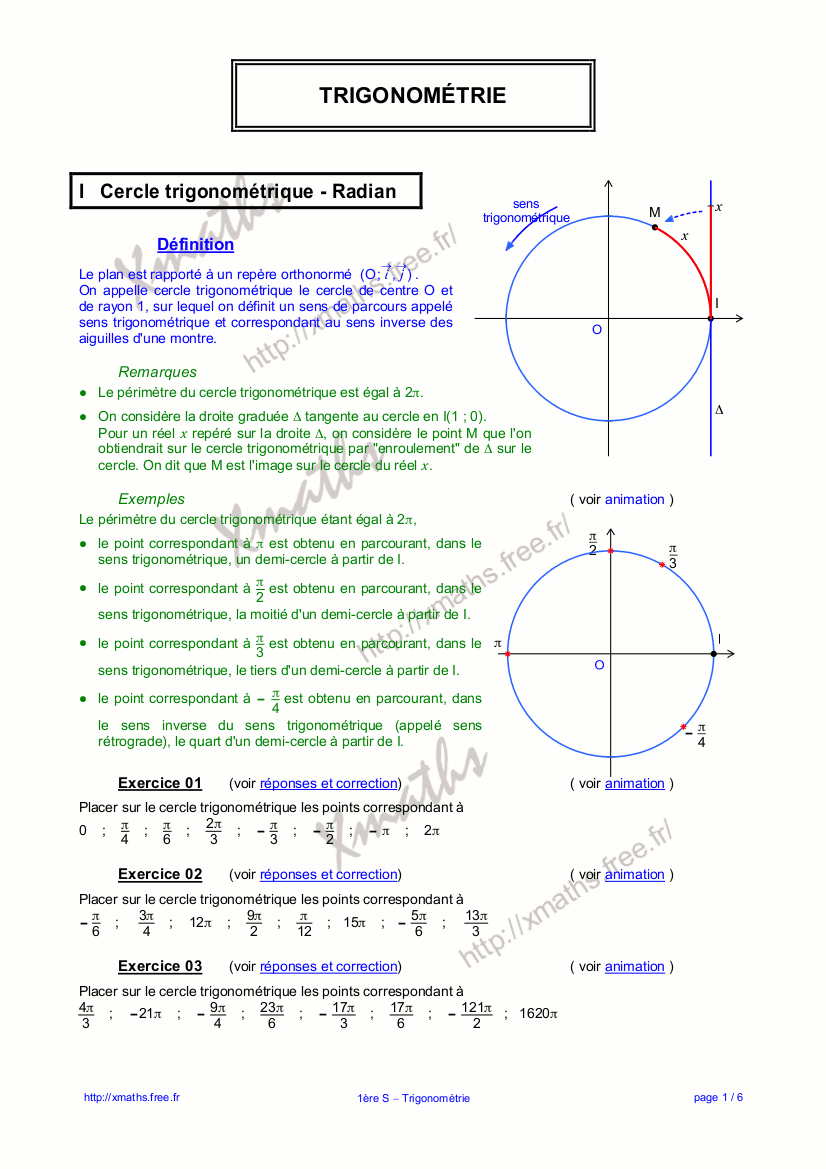
on rappelle ici et on complète les résultats énoncés au lycée. l’objectif à viser est la technicité. pour cela, il faut : Œ connaître par cœur les différentes formules de trigonométrie, savoir à quel moment s’en servir. en ce qui concerne le premier point (Œ), au cours de l’année de mathématiques supérieures, on doit apprendre

Vu sur mathsbook.fr
formulaire de trigonométrie circulaire. b cotan(x). k sin(x) мн cos(x) = abscisse de m tan(x) sin(x) = ordonnée de m. Ł tan(x) = ah cos(x) a cotan(x) = bk eix = zm. Π sin(x). pour x É, tz, tan(x) = cos(x). valeurs usuelles. cos(x) et pour x É tz, cotan(x) = . enfin pour x z, cotan(x) = sin(x). z tan(x). x en . x en rd. . sin(x).

Vu sur xmaths.free.fr
fonctions trigonométriques usuelles (cosinus, sinus, tangente) que le lecteur a sans doute déjà rencontrées sur le cercle trigonométrique, la mesure en radians d’un angle est égale à la mesure en unités de longueur de .. inpl . . en utilisant les premières propriétés mises en évidence dans ce cours, cos.

Vu sur mathsbook.fr
automaths. . le sinus, le cosinus et la tangente d’un angle n’ont pas d’unité. trigonometrie. emilien suquet, suquetautomaths. i cosinus, sinus et tangente d’un angle aigu. dans un triangle abc rectangle en a, on définit le sinus, le cosinus et la tangente de l’angle aigu. abc de la manière suivante :.

Vu sur previews.fichier-pdf.fr
il faut remonter jusqu’aux babyloniens, ans avant notre ère, pour trouver les premières traces de tables de données astronomiques. car à la base, la trigonométrie est une géométrie appliquée à l’étude du monde, de l’univers et est indissociable de l’astronomie. mais on attribue à hipparque de nicée ( ; ) les
Vu sur mathsbook.fr
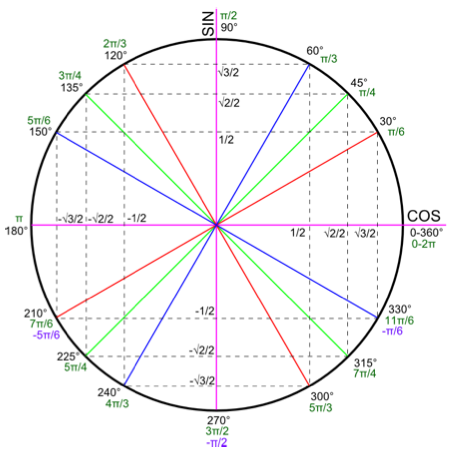
formules de trigonomÉtrie : sinus, cosinus, tangente. . les formules de base : cos x sin x = cos(x π) = cos x sin(x π) = sin x cos x sin x x cos(−x) sin(−x). −x. nous avons les formules suivantes : cos(−x) = cos x sin(−x) = −sin x. on retrouve graphiquement ces formules à l’aide du dessin des angles

Vu sur mathsbook.fr
nous le renvoyons à ses cours de l’enseignement secondaire. il ne faut pas considérer ce document comme une bible! d’une part, il ne s’agit pas de notes de cours. les notions ne sont pas toujours abordées dans le même ordre que lors de leur approche en classe. d’autre part, il est certainement pourvu de nombreux
Vu sur pi.ac3j.fr
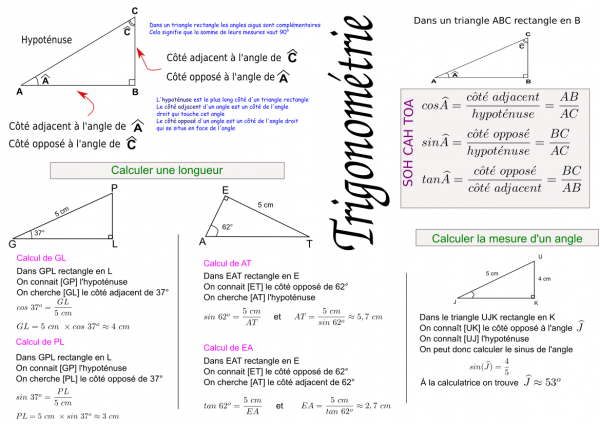
chapitre n° : « trigonométrie ». i. rappels. vocabulaire. • un triangle rectangle est un triangle qui possède un angle droit. • l’hypoténuse est le côté situé en face de l’angle droit : [bc ] . • les autres côtés sont appelés les côtés de l’angle droit. • par rapport à l’angle. cba : [ ab] est le côté adjacent et [ca] est le côté.
Vu sur ekladata.com
d’algèbre et de trigonométrie. mrenf. jeanphilippe javet . malgré le soin apporté lors de sa conception, ce support de cours contient certainement quelques erreurs et quelques coquilles. de participer à .. bertrand russell. . plus d’info sur : georgesbarthélemy/implication_logique_mathématiques.pdf









